When I was an instructional coach, the question I received most often was “How do you have students work in groups without it turning into chaos?”
After nearly three decades of using cooperative learning groups in my own classes, I will answer that question here along with these others:
-
-
-
Why Group?
-
Which Group Structures?
-
How to Manage Groups?
-
When to Group?
-
-
Why Group?
Before we get into the details of conducting collaborative groups in class, we need to understand the benefits of cooperative learning. Why should we use student groups in our teaching anyway? There are several solid reasons.
The first one comes from Scott Freeman in his 2013 article by the National Academy of Sciences, in which he states:
“Active learning is the empirically validated teaching practice in regular classrooms… It emphasizes higher-order thinking and often involves group work.”
So the science has settled it. This is not a matter of using more ‘touchy feely’ instructional techniques. Instead, active learning through group work is a bonafide method of instruction. The efficacy of collaborative learning can be found even at the college level, as was reported by the Mathematics Association of America in 2015:
“Failure rates under traditional lecture are 55 percent higher than the rates observed under more active approaches to instruction.”
In other words, you can cut your failure rates by a third by introducing active learning into your instruction. Furthermore, the Journal of Engineering Education promoted more active learning almost 20 years ago when they claimed that:
“Students will remember more content if brief activities are introduced to the lecture.”
So yes, group work is a means to better teach mathematics, but it is also used to teach other skills as well. The Cornell University Center of Teaching Excellence discovered that the following soft skills can be instilled by a more collaborative classroom enviornment.
- Higher-Level thinking
- Oral Communication,
- Self-Management, and Leadership Skills.
- Student-Faculty interaction.
- Retention and Responsibility.
- Diverse perspectives.
- Preparation for real life social and employment situations.
The final argument for using student groups for instruction is that collaboration itself is something that we should be teaching. The business community has been wanting the education system to graduate students who can more than just play nice together, but who can also work as a team to generate a quality product. This idea can be seen in the international survey conducted by the World Economic Forum, The 10 Skills You Will Need to Thrive in the Fourth Industrial Revolution. Employers were asked in 2015, what skills do they consider most valuable in an employee, and what they predict those skills will be 5 years later in 2020 (2 years ago as of this post). The Top 10 are shown below:
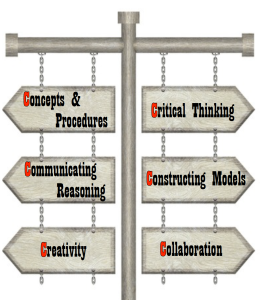
These lists align tightly with the now famous 4 C’s of 21st Century Education: Critical Thinking, Communication, Creativity and … Collaboration. These skills are becoming increasingly valued because they cannot be automated, so these four attributes will need to be developed in our students. And collaboration makes the list. In other words, we should not only be using collaboration to teach math; we should also be using math to teach collaboration.
So in answer to our first question, Why Group Work?
Research and the 4 C’s both claim it is imperative.
Which Group Structures?
There are three predominant group structures:
- Homogeneous: Students of one group are all of the same ability. The A students work with A students; F students work with F students.
- Heterogeneous: Mixed ability levels. A group of four is comprised of one high performing student, one low, and a couple of middle range students.
- Random: Students are randomly assigned a group.
There are three math education professors who each emphasize a different model.
I was originally trained as a student teacher to use heterogenous grouping, promoted by Dr. Boaler. Dr. Treisman got to me, though, as a young teacher, so I spent most of my career using the homogeneous model with a great deal of success. Dr. Horn, who wrote Strength in Numbers, supports random grouping. Three highly regarded professionals giving me conflicting advice made me curious as to which was the best model. I researched the topic and found out two things at the time:
- The Grouping Structure didn’t matter; it was grouping itself that was making a difference over not grouping at all. Also, different students respond differently to the different grouping strategies. In addition, some tasks lend themselves better to one method over another.
- It is the Group-Worthy Task that really makes the difference. When students are grouped, we teachers tend to give them more rigorous tasks than when they are working independently.
Then, after years of thinking I had this matter settled in my head, Dr. Peter Liljedahl published Building a Thinking Classroom in which he claims that visibly Random Grouping is superior. My colleague, Mary Vongsavanh, and I tested this out recently in a co-teaching opportunity and sure enough frequent randomization of the groups generated a great deal of high-level dialogue and positive group behaviors.
The one exception, was when we graded the task. In these situations, the stress of the A-students overwhelmed the less dutiful F-students, who just let the high-performers take over the work… which is exactly what Dr. Treisman warned against. For the graded tasks, then, we found that the homogeneous grouping worked best.
Therefore, the answer to our second question, Which Group Structures?
Group randomly, using group-worthy, high cognitive demand tasks. When the task is graded, though, group homogeneously.
How to Manage Groups? 
Students don’t naturally know how to collaborate productively, which is why simply saying “Turn and Talk” produces either silence or chaos. This failure subsequently discourages teachers from implementing group work again. A few simple tactics can teach students how to collaborate and make the teacher feel like a pro at facilitating group work. The list of parameters that promotes productive student collaboration is short and very doable:
-
-
-
-
-
-
-
Norms
-
Vigilance
-
Accountability
-
-
-
-
-
-
Since students don’t know how to collaborate productively, they need to be taught this skill. In a training for my former district, Dr. Juli Dixon of University of Central Florida, shared the following set of norms for student groups:
- I will explain my thinking.
- I will listen to the thinking of others.
- I say something if disagree or don’t understand.
I shared these on Twitter with the following caption, “What if instead of the classroom rules being ‘No Hats, No Food, No Gum,’ the rules were these instead?” It was the most retweeted message I have ever posted.
My short version of these Norms is:
- All Voices.
- All Present
- All In
How important are Norms? Well, we know creating them is one of the first moves in forming PLC teams. So, if adults need norms in order to work together… what might children need?
Once you have students working together, you need to be vigilant about monitoring the groups. A friend of mine, Nanette Johnson, coined the phrase ‘Group work only works when you work the groups.’ You can’t push desks together, hand them all a sheet of paper and go sit at your own desk to grade papers, and expect the students to be productive. You need to walk the room. My experience says that for the first few weeks of this, you will spend far more time enforcing the norms than discussing math. It is helpful to have the norms posted somewhere to easily reference. Eventually, the students will adapt, and you will be able to focus on the math.
The third principle that will enhance the group work in classes is Accountability. Be every clear and tight on the product the groups are to generate and the time they have to complete the task. In other words, simply saying “turn and talk” doesn’t work. What does work are instructions like, “In 3-minutes, your group is to write the solution to this equation, showing all the steps, on one whiteboard.” Remember, be vigilant by making sure that all groups are completing the task properly.
Therefore, the answer to our third question, How to Manage Groups?:
With Norms, Vigilance & Accountability.
When to Group ? 
As much as group work is being under utilized in classes, it is possible to also over use it. There will always be a need for direct instruction. It is just that currently, that is all that most students experience, especially in math. So where is the sweet spot? Just how often should teachers have students learn collaboratively? I have heard and read everything from 55% to 65% of the time, therefore, I’m advocating for the median… 60% of the time. Rather than saying that means ‘3 out of every 5 days a week,’ or multiplying the number of instructional minutes by 0.6, let’s simply say that we should be implementing group work most of the time. 40% is still a large portion dedicate to direct instruction. We can then say that group work should be used most of the time and direct instruction is still used a lot of the time.
In fact, the meta-research shows that we want to keep both components in our instructional repertoire. John Hattie’s Visible Learning list of effect sizes supports this idea of a balanced approached between active learning and lecture oriented lessons.
Cognition Task Analysis: 1.29
Discussion: 0.82
Problem Solving: 0.68
Direct Instruction: 0.60
Cooperative Learning: 0.40
By why is this balanced approach tilted towards cooperative learning? I see the reason for group work taking most of the instructional time is that it is slower than direct instruction. So why should we use it if we can the job done faster another way? That answer lies in the purpose of the instructional model.
Direct instruction is most effective when teaching procedural skills, however, it is very ineffective when teaching problem solving skills. No one learns how to solve problems by watching someone else solve problems; they learn it by solving problems (see our interview with Dr. Jon Star), and this is best done in peer groups. In terms of the teaching progression of Concepts-Procedures-Applications, group work is best used at the bookends, when developing conceptual understanding and higher-order thinking skills. These phases still utilize direction instruction when concluding lesson tasks, however, the mathematical conventions are not universally discovered by student consensus, so they are best taught by direct instruction.
For example, in teaching the addition of fractions, one may start with a Clothesline Math lesson to develop the need to find a common denominator (conceptual) which would involve students posing and critiquing strategies in pairs and groups, with the teacher concluding the lesson with the most efficient method. Subsequent lessons would involve examples and notes on the algorithm for adding fractions with unlike denominators, and another for guided practice, both delivered by direct instruction with individual student work. This should then be followed by a lesson posing a task which requires an application of the addition of fraction. This activity would best be started by the students solving individually first, then discussion in groups, with the conclusion being a teacher-led student reflection on the solution. This progression would entail a significant amount direct instruction, and an even greater amount of group work in a balanced instructional model.
Finally, the answer to our fourth and last question, When to Group?
Most of the Time, and when teaching concepts and applications.
In Summary,
Q: Why Group?
A: Research and the 4 C’s both claim it is imperative
Q: Which Group Structures?
A:
Q: How to Manage Groups?
A: With Norms, Vigilance & Accountability.
Q: When to Group?
A: Most of the Time, and when teaching concepts and applications.
















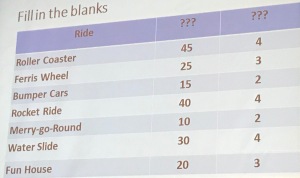
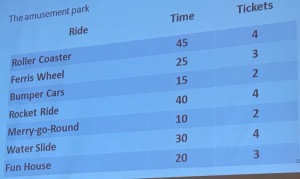





 I have summarized each session with some simple (•) bulleted notes,
I have summarized each session with some simple (•) bulleted notes, 
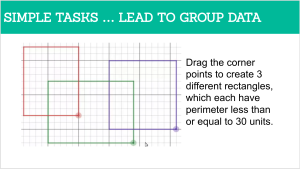
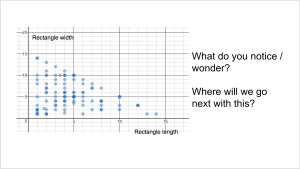
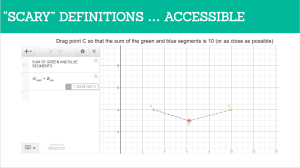












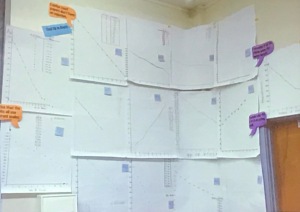

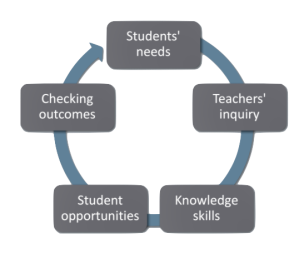

 She then shared how she grouped them (which is what the color scheme was for). The idea was to take ALL the things that we want teachers to know and do and rather than create a checklist for them, cluster these concepts into Themes or Essential Elements and have teachers learn that.
She then shared how she grouped them (which is what the color scheme was for). The idea was to take ALL the things that we want teachers to know and do and rather than create a checklist for them, cluster these concepts into Themes or Essential Elements and have teachers learn that.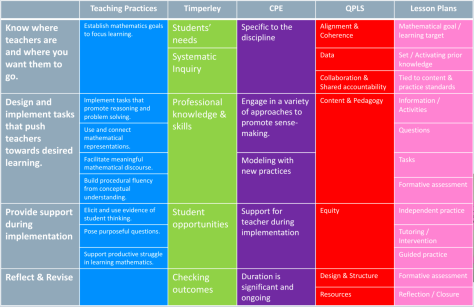


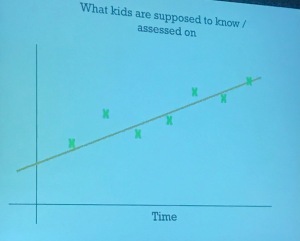 vs what they are assessed on.
vs what they are assessed on.
 Example: Make the smallest (or largest) difference by filling in numbers 1-9 no more than one time each.
Example: Make the smallest (or largest) difference by filling in numbers 1-9 no more than one time each.




 There were at least 5 sessions at NCTM Annual in which the Clothesline was a part or the focus of the presentation.
There were at least 5 sessions at NCTM Annual in which the Clothesline was a part or the focus of the presentation. 
 Fun Sidenote: The ceiling rafters and the carpet print of the convention center had the same Geometric Pattern. I am sure there is lesson to be created out of this.
Fun Sidenote: The ceiling rafters and the carpet print of the convention center had the same Geometric Pattern. I am sure there is lesson to be created out of this.











 Tracy shared a list of questions to facilitate the explicit development of mathematical intuition. They can be found in her book and companion web site:
Tracy shared a list of questions to facilitate the explicit development of mathematical intuition. They can be found in her book and companion web site: 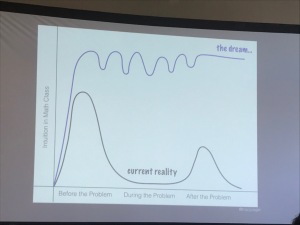

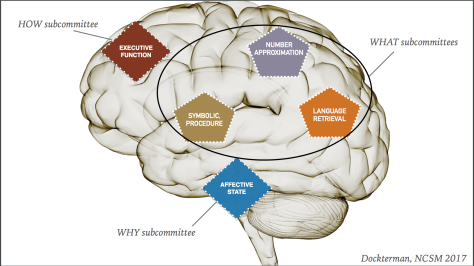
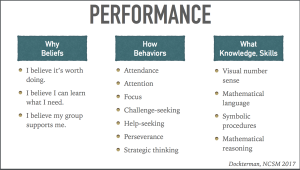





















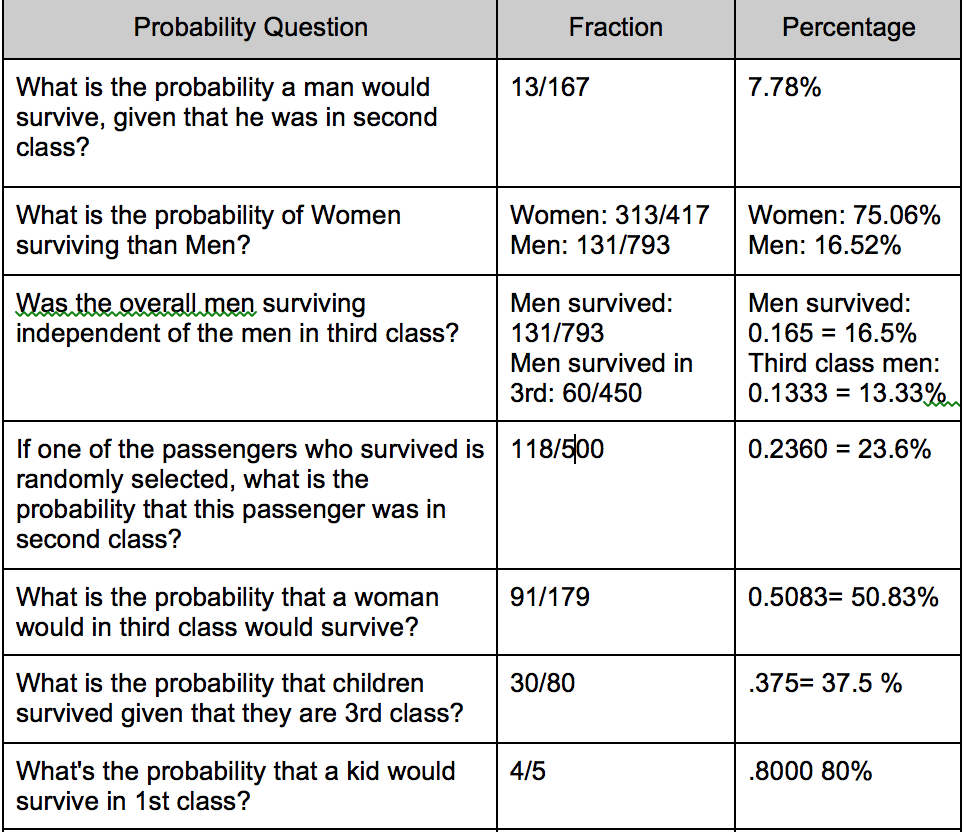



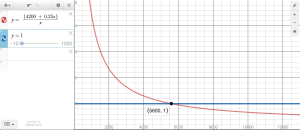
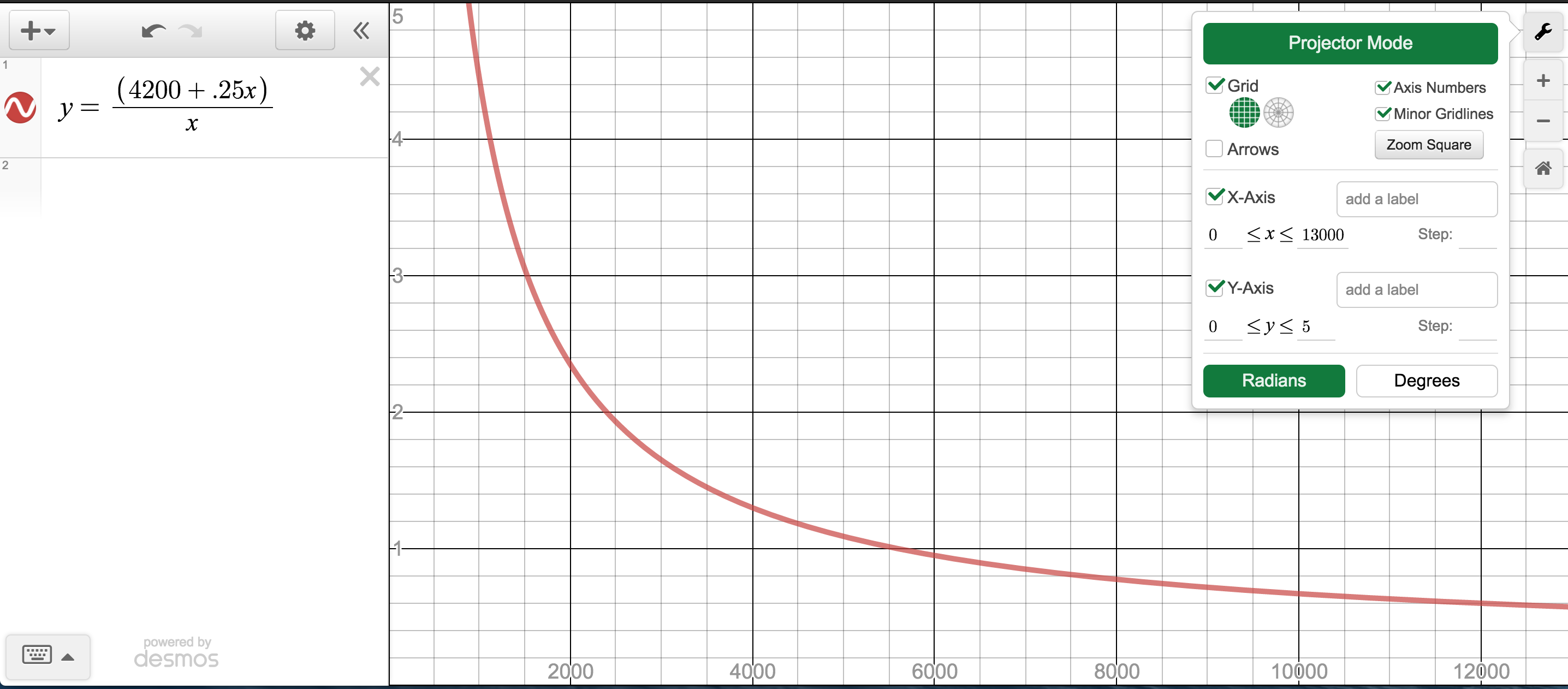

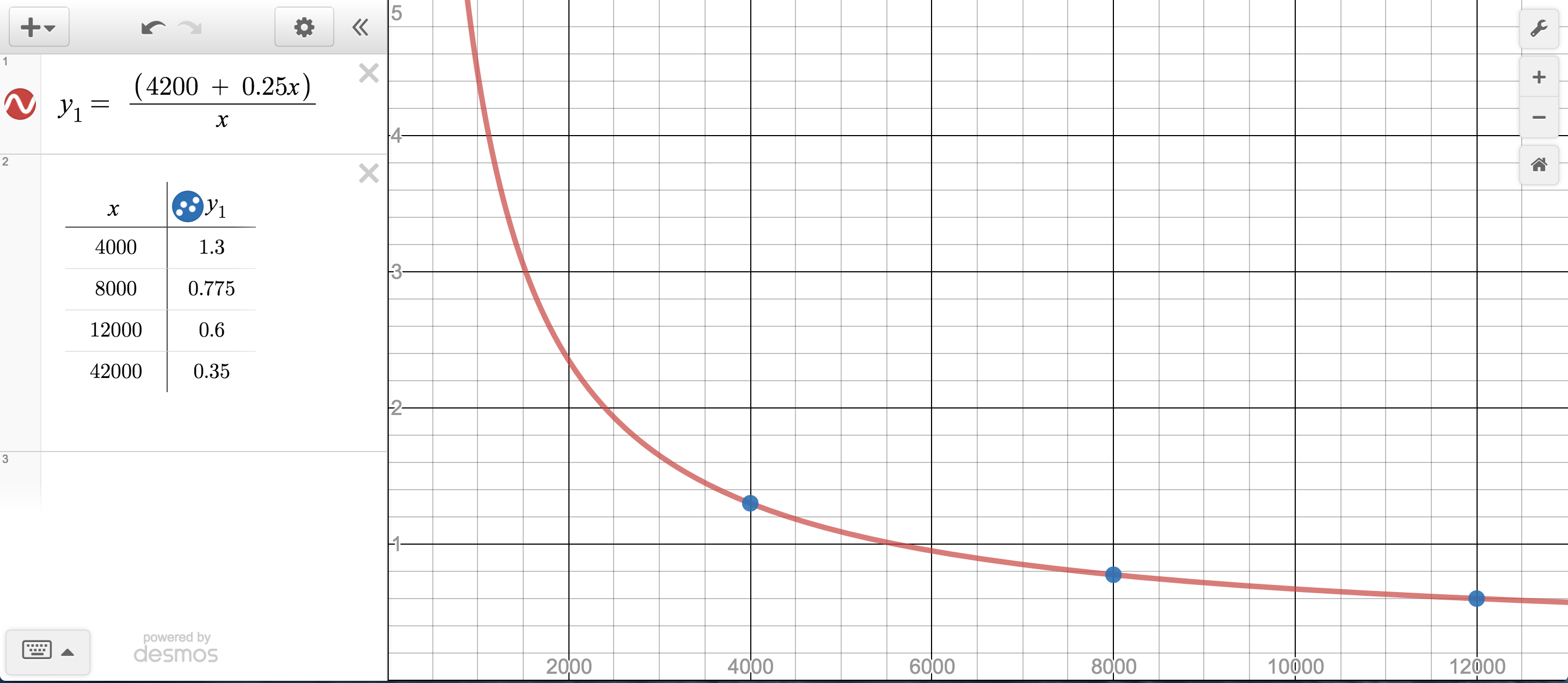
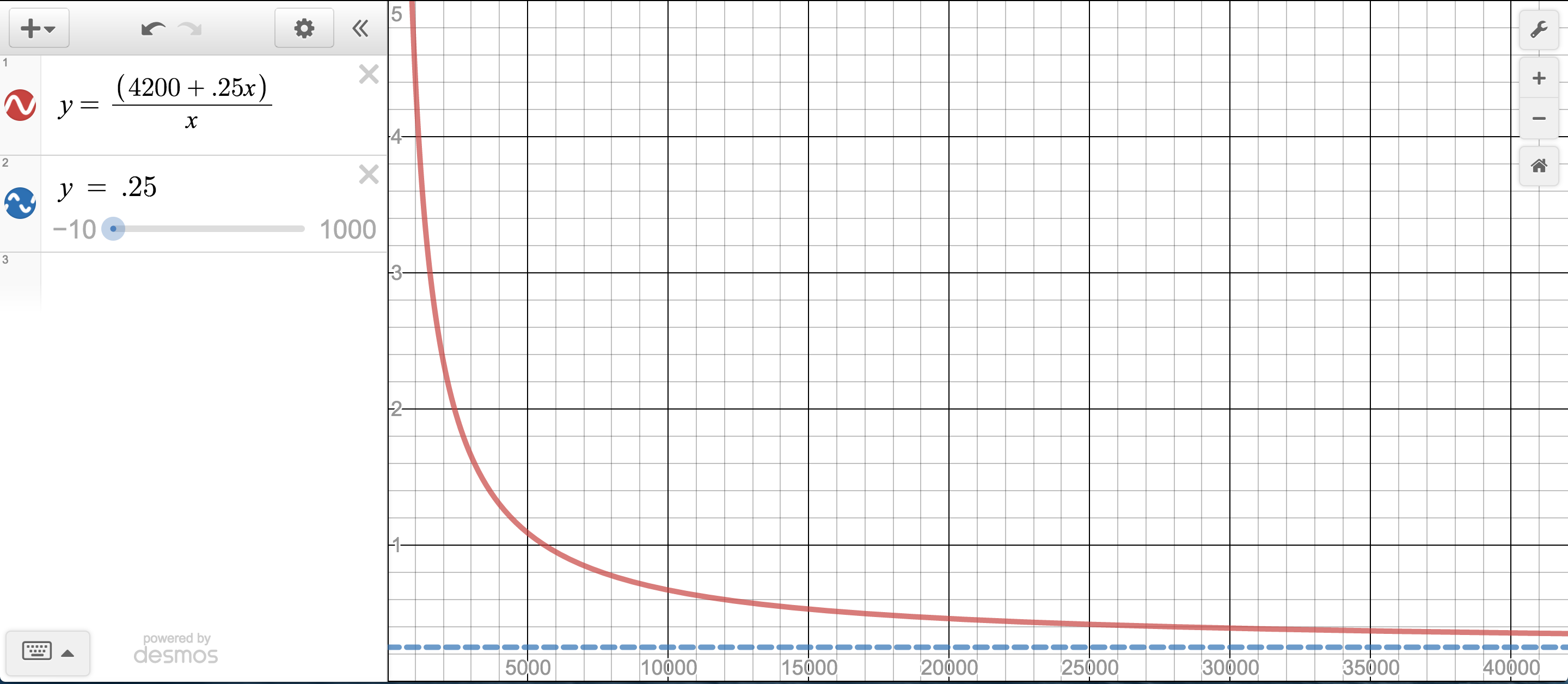

 I added two components to a lesson task on rational equations.The first was an idea called, Hint Cards, shared by
I added two components to a lesson task on rational equations.The first was an idea called, Hint Cards, shared by