Category Archives: 180 Blog Geometry

180 Blog Geometry, Blog

Titanic Two-Way Frequency Tables

5 Comments

This outstanding lesson on two-way tables was born out of three sources: a fantastic resource from Illustrative Math, the award-winning movie, Titanic, and an empowering presentation by Chase Orton (@mathgeek76 ). At CMC-North, 2015, Chase shared the “Lived or Died” two-way table, which does a fantastic job of hooking students and introducing them to the concept of determining dependence from categorical data; plus he offered some follow-up activities. While Chase’s lessons claim to be for 8th grade standards, Illustrative Math provides lesson plans and student prompts for the high standards regarding two-way tables. The movie clips help frame the historical  contexts and the mathematical questions to be answered with the tables.

Here is how I put all these elements together into one lesson.

Titanic Day 1

Dual Objective: Reason Quantitatively in using two-way tables to  determine probabilities of survival.

Warm-up:
1) 320 is what percent of 710?
2) What do you Notice and Wonder about this following 2-way frequency table?

The obvious notice was the number of men that died. The common wonder was in regards to the event that caused so many deaths. The conjectures ranged from disease to war. After the enthusiastic discussion, I shared this video clip from the movie, Titanic.

So now we know… the disastrous event represented in the data table was the sinking of the Titanic. I disseminated the handout that offered a new two-way table relating to that fatal day.

The students were very curious about why the total number of survivors and deaths were so significantly different from the previous table. We all concluded that this table strictly showed passenger data, and the other one must have included data for the crew as well.

The prompts today focused on the basic skill of calculating probabilities from the table, specifically, the probabilities of event A, event B, events A and B, event A given B. Namely,

P(A), P(B), P(A and B) and P(A|B)

For example,

  • If one of the passengers is randomly selected, what is the probability that this passenger was in first class?
  • If one of the passengers is randomly selected, what is the probability that this passenger survived?
  •  If one of the passengers is randomly selected, what is the probability that this passenger was in first class and survived?
  • If one of the passengers is randomly selected from the first class passengers, what is the probability that this passenger survived? (That is, what is the probability that the passenger survived, given that this passenger was in first class?)

Today was a great prelude to the next lesson on determining dependence.

Titanic Day 2

Dual Objective: Reason Abstractly in using two-way tables to  determine dependence between passenger class and survival on the Titanic.

I noted to the students that our target was very similar to yesterday’s in that we were still dealing with the same content (2-way tables), with the small change being in the Mathematical Practice. Today we were changing the Reasoning Quantitatively to Reasoning Abstractly. This meant that yesterday we focused on thinking about numbers, and today we were going to be thinking about relationships.

Warm-up: (yesterday’s skill and notation)
1) What is the probability that a passenger was in second class? P(A)
2) What is the probability that a passenger survived? P(B)
3) What is the probability that a passenger was in second class and survived? P(A and B)
4) What is the probability that a second class passenger survived? P(A|B)

After reinforcing yesterday’s lesson, I showed this second video clip from the movie Titanic.

This scene is an artistic interpretation of the treatment of third class passengers, but is this attitude towards people in steerage historically accurate? Did the wealthy receive preferential treatment in evacuating the ship? Even though we were not there over 100 years ago, we can still determine the truth, because we have data!

So, I disseminated handout #2 that offered the same two-way table as yesterday. The major idea here is to determine if the chance of survival of all passengers was different from the chance of survival for a first class or a third class passenger.  In other words, was the probability of survival dependent or independent of passenger class. Namely, is P(A|B) = P(A).

Since the general chance of surviving was 38%, but the probability of survival for first class passengers improved to 62% , while that for third class diminished to 25%, the students concluded that survival was indeed dependent upon class.

Then it was time for the students apply what we just learned to another question of dependence aboard the Titanic. I showed this video clip.

Again, we needed to test the validity of this artistic interpretation of history with data … and our new skills. (handout #3) Was it truly “women and children first?”

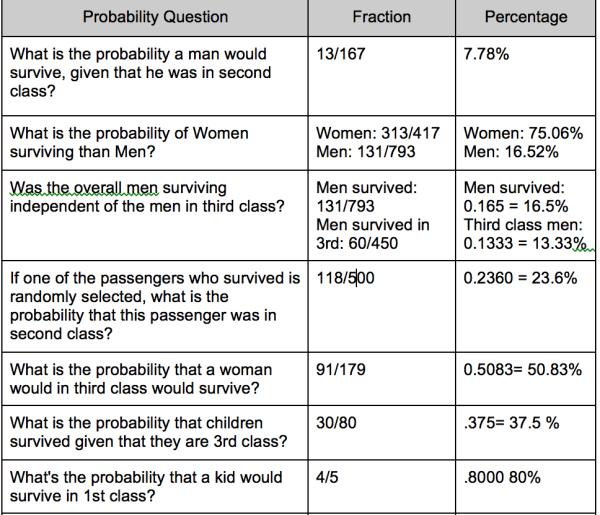
A colleague of mine, Kristan Morales (@KristanMorales1), did this lesson and asked the students to offer questions that can be asked from the table, and collected the responses in a google doc. Here is a small sampling of the student generated questions:

Titanic Morales

Day 3 … Chores & Curfews

Dual Objective: Use Structure in creating a two-way table and use the table to Judge the Validity of an Argument regarding dependence.

On the third day, I had the students practice with some more relevant (and less traumatic) contexts that Chase provided in his session. I loved how Chores & Curfews tied in Venn Diagrams to the probability conversation while requiring students to complete their own 2-way table.

All the work involved here empowered the students with the tools and information needed to determine the validity of the claim that those with chores were more likely to have a curfew.

The following are the various materials available for this lesson, from…
Chase Orton: Titanic Plus
Illustrative Math: Titanic 1, Titanic 2, Titanic 3
Chris Shore (Me): Titanic All, Chores & Curfews

Personal Note: The executive producer of Titanic, John Landau, was my pledge father in my fraternity at USC.

180 Blog Geometry

Portfolios & Music Cues

2 Comments

Day 3, Fri Aug 14, 2015

Cover Portfolio GeomMusic Cues: I heard this great idea from Matt Vaudry at Twitter Math Camp ’15, on using music cues for certain transitions and activities. Matt uses MANY different songs, but I choose to use only three:

1) The Mission Impossible theme song for preparing for class: My students each have a Portfolio (3-Ring Binders), a workbook, and a whiteboard. Each pair of students has a “Tool Kit.” All of these must be at their desks, plus their cell phones must be placed face down on the outside corner of the desk. Matt gives them one minute of the song; since my students have to retrieve materials from the portcase, I give them two minutes.

2) The Benny Hill theme song for cleaning up: They must get everything put away and sit back in their desks, so we can debrief the lesson (The Brain Surgeon’s Wrinkle Sprinkle)

3) The Dun-Dun-DUN sound for announcing the instructional target. (Which we will start next week.)

We practiced these back to back a few times until we got it down. It works amazingly well! Thank you Matt.

Portfolios: I require students to keep a portfolio in class. The portfolio has a cover sheet that intentionally refers to them as “Genetically-Coded Math Experts.” I used today to reinforce the 6 C’s as our ultimate goal of the course, which I introduced yesterday. The portfolio is structured around these six values as is my grade book. My students from last year, received their portfolios back from Algebra 1; the new students received a free binder from an anonymous donor. We built the portfolios section by section.

I saved the students the grief of going through the syllabus. I gave them the Course Overview to read on their own (which they won’t) and have their parent’s sign (they won’t read it either) and return to their portfolios by the end of next week. Rather than bore them with the grading policies all at once, I discuss them briefly when they arise in class. (e.g. Discuss homework when the first homework assignment is assigned.)

Wrinkle Sprinkle

  • The 6 C’s
  • We are going to learn how to think
180 Blog Geometry

First Day’s Transformation Question – Geometry

Leave a comment

Day 1 & 2, Thurs Aug 13, 2015

Class Pic{My school has a special tradition of activities on the first day in order to promote our school motto: S.P.I.R.I.T., Scholarship, Passion, Involvement, Reflection, Integrity, Teamwork. Teachers do not officially see their new students until Day 2}

Greeting the Crew: I greeted each student at the door with a high-5, inspired by Glenn Waddell (@gwaddellnvhs). All my students who finished the year with me last year, returned, with the addition of 13 new ones. These is a great bunch!

Opening Quiz on the 6 C’s: I always start every year by answering the transformation question: “How will you (the students) be different in June than you are now, because of my class?” This year I am answering that question with the same 6 C’s that I launched last year. My Claims-Based grading system and the students portfolios are structured as such also. These C’s are based on the Smarter Balance Claims and the 4 C’s of 21st Century Learning.

  • Concepts & Procedures
  • Critical Thinking
  • Communicating Reasoning
  • Constructioning Models
  • Creativity
  • Collaboration

I gave the students the blank copy of the quiz below, and told them this was not to be graded nor was it a test of their previous knowledge. It was like a movie trailer of things to come, but I still wanted them to give me their best shot. I then gave them my standard 3-response speech.

As a mathematician I cannot always give an accurate response; I cannot always give a complete response; but I can always, always, always give an intelligent response. Blank is not intelligent.

I pressed them to give me something… numbers, equations, drawings … anything intelligent.

Opening Quiz Pic Geom

They worked on these independently, then in groups, then as a class. I wanted to model this process right away, because I use it often.

Last year with this group I fielded the “I feel stupid comment;”  this year it was the, “She is really smart” comment. This gave me the opportunity to once again, press upon them that they are all smart; I’m just here to make them all smartER.

I posted on the board several of the responses that I saw on the student papers. I shared that these are the 6 C’s of the course. That these 6 things are really what they are here to learn. So I didn’t even answer the questions… that will come later in the course. I just wanted to highlight & explain what the first 4 C’s meant, and the other two would be woven throughout. I said that these things are what mathematicians really do, and that I am paid big bucks to get them all thinking like this in 10 months.

Introductions: I have each student briefly state their name and something interesting about themselves. I use the time that they are talking about the point of interest to review the names in the class, so at the end, I can recite all the names in class. Since I already knew most of the kids, this was easy.

I then shared that the reason that we did math first is because that is what we all about.. learning math … not collecting points… and the math was being learned by them, so those are the two most important things going on in the room on any given day. I also assume they can read the grading policy if I gave to them I didn’t have to bore them with it. Since this is the last class of the day, they all thanked me profusely, for that’s much of what they experienced their first day.

The Brain Surgeon: Last year I implemented some ideas that I came up with to promote Carole Dweck’s Growth Mindset findings. One of them was the Brain Surgeon, whose responsibilities are to read the target for the day, and lead the Wrinkle Sprinkle at the end of the period.

Wrinkle Sprinkle: This is another vehicle that I created to promote the Growth Mindset. My students from last year, knew the routine. I explained to the new students that when we learn, we don’t just shove stuff in our brains, but that the brain cells actually grow and connect to each. I joked that it was like getting a new wrinkle on the brain, and that we were into growing our brains in this class. Therefore, at the end of each class, we will debrief what we learned and write it on the board.

  • How to Model a situation with a drawing (From questions #2 & 4 on the quiz)
  • Logan can do a back flip
  • Two people have last names in Spanish that mean a place, and another has a Spanish last name that means cow.

It was a high-spirited, fun first day. The students have me pumped for the year!